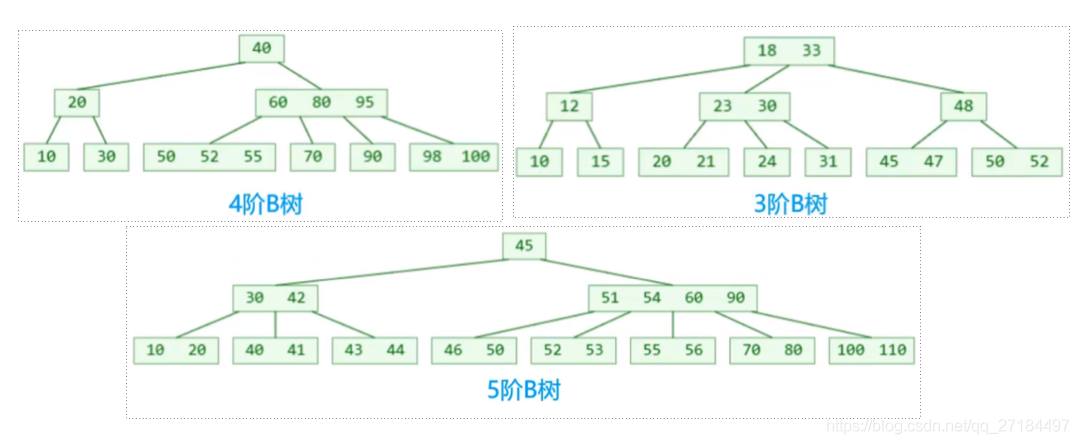
在数据结构中,树这个概念用的非常多,特别是在Map 存储中其实就是一个树的概念, 这种结构也叫树结构,跟线性结构不同,线性结构就是链表,就是一条线就可以表示完了,但是树状结构的分支会有无限多,我们本章就是只要理清楚红黑树的概念,但是要想理清楚红黑树就必须得先知道普通的树和B树的结构,理清楚这两个树可以帮助我们更好地理解红黑树,因为红黑树和B树是可以互相转化的!
树
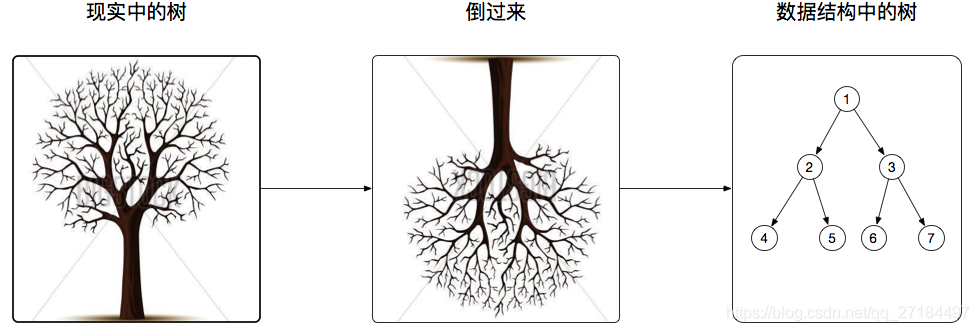
树没什么好说的,一个图你们就明白了树是怎么回事了!我们入场生活中的树的根是在下面的,但是在数据结构中,树的根节点一般是在上面的, 所以在图片中做了一层转化;我们只需要知道什么是树就可以了;
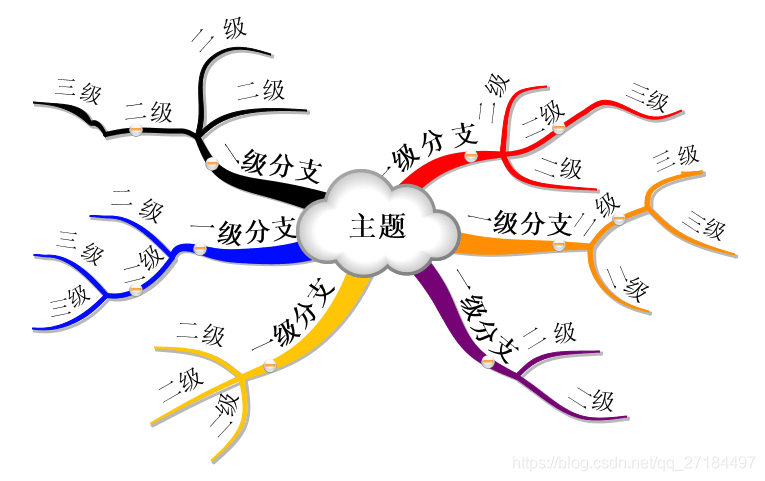
我们工作中用到的思维导图本质上也是树形结构
二叉树
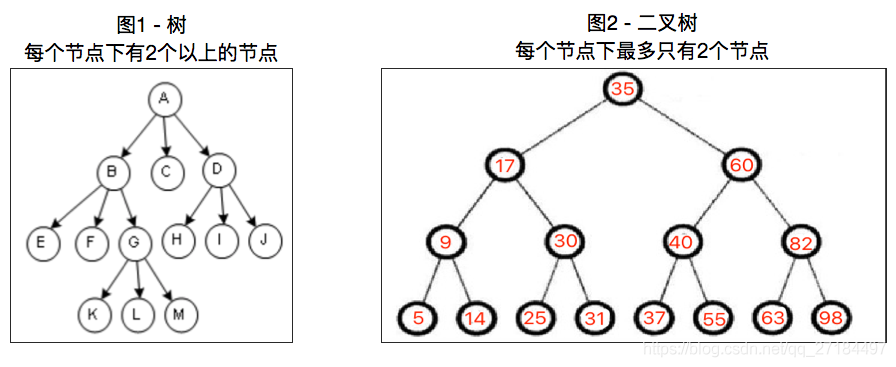
正常情况下,每棵树的树干都有多个树枝,而二叉树只有2个节点,区别如下:
二叉搜索树
二叉搜索树是二叉树的一种,是非常广泛的二叉树,又被称为二叉查找树,二叉排序树(没错,既然叫排序树,那么它就是有序的)
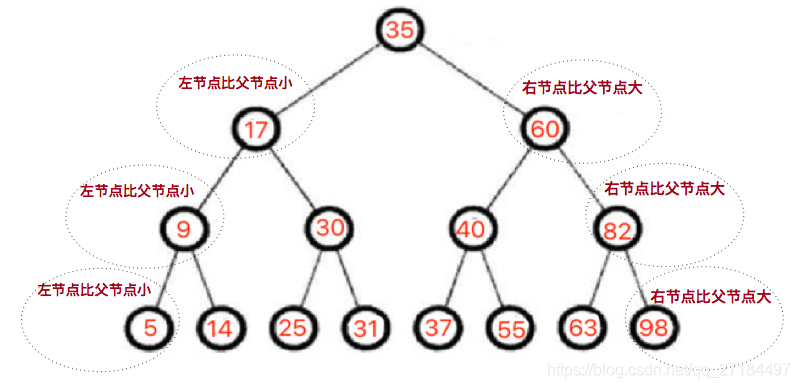
二叉搜索树的特性如下:
- 除根节点之外,任意一个节点的2个子节点,左节点的值一定比父节点小,右节点的值一定比父节点的大,
- 它的左右子树也是一颗二叉搜索树
- 二叉树可以大大提高数据搜索的效率
- 二叉搜索树存储的元素 必须是可比较性的 (比如 int、long、double 等。。。。。 如果是自定义类型,需要指定比较方式)
B树 (B-Tree 、B-树)
B树是一种平衡的多路搜索树,多用于文件系统,数据库的实现,B树特性:
- 1个节点可以存储超过2个元素,可以拥有超过2个子节点,
- 拥有二叉搜索树的一些性质
- 每个节点的所有子树高度一致
- 比较矮
B树子节点规则
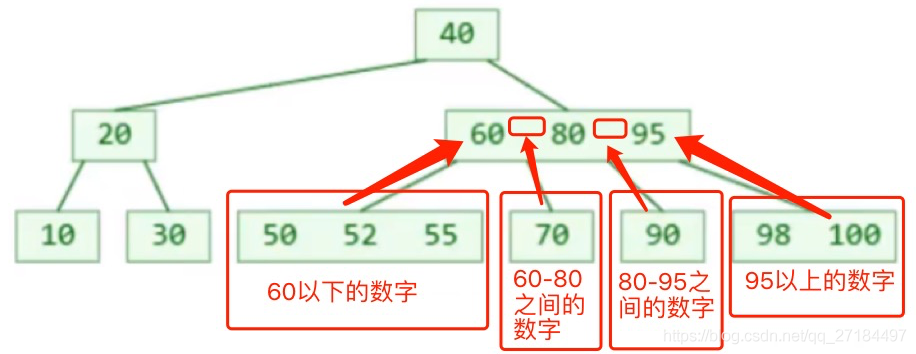
如果B树内一个节点中有多个元素,那么每个元素的数值之间都会有一个子节点,如下图,
下面的一个节点中有3个元素,分别树60、80、95,那么对应就会有4个子节点,分别是:
- 60以下的值 (节点1)
- 60~85之间的值(节点2)
- 85~95之间的值(节点3)
- 95以上的值(节点4)
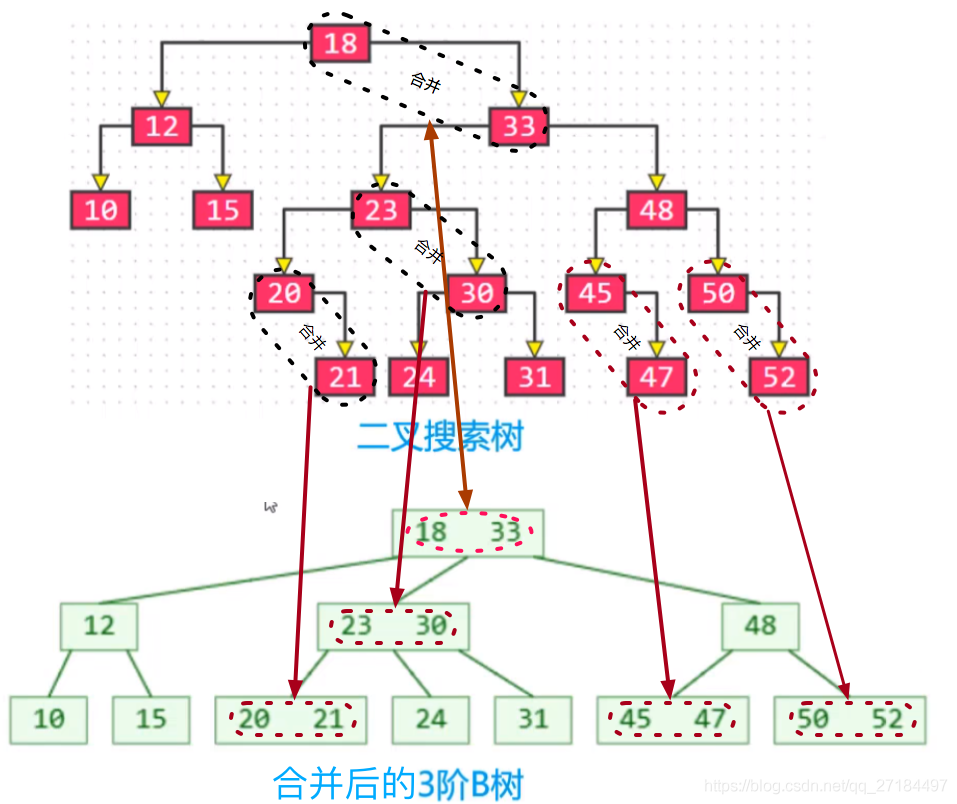
B树和二叉树相互转换
B树和可以二叉树相互转换,通过合并二叉树来得到B树,当然,不只有这一种合并方式,这里只是举例转换的方式;
红黑树
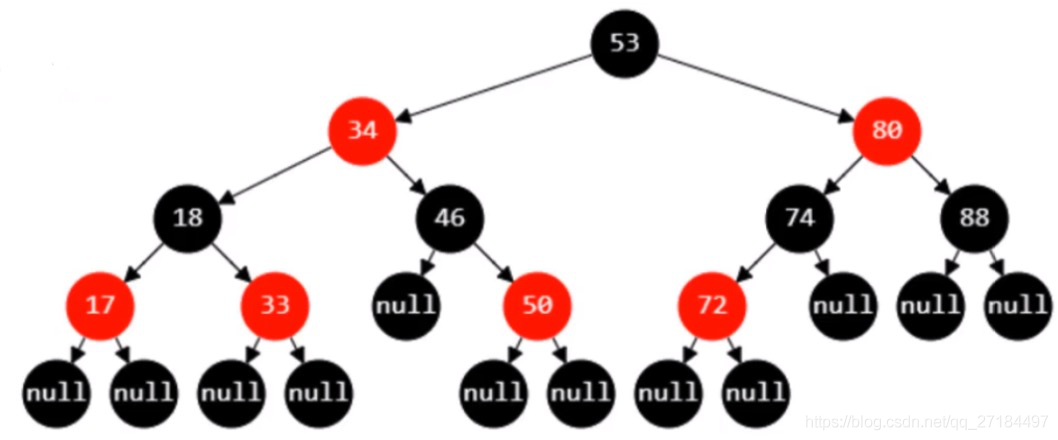
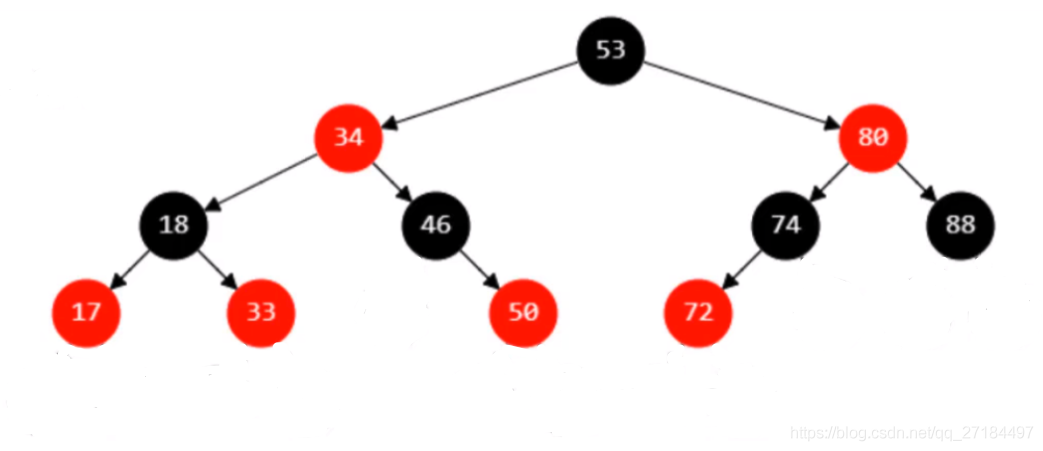
红黑树也是一种自平衡的二叉搜索树,以前叫做平衡二叉B树,是平衡二叉树的一种,红黑树必须满足以下5条性质
- 节点要么是 RED ,要么是 BLACK;
- 叶子节点(外部节点、空节点)都是 BLACK,就是每个 RED 节点下都会增加2个空的 BLACK,单个子节点的会自动增加一个空的 BLACK 节点,(注意:这些为 null 的 BLACK 都是假想出来的,写代码的时候不需要把这些空节点加进去)
- 根节点都是 BLACK
- RED 节点的子节点都是 BLACK
- RED 节点的 parent 都是 BLACK
- 从根节点到 叶子节点的所有路径上不能有2个连续的 RED 节点
- 从任一节点到 叶子节点 的所有路径都包含相同数目的 BLACK节点
↓